机器学习

K-Means

方以类聚，物以群分。
                    ——《易经》

聚类算法KMeans是无监督学习的杰出代表之一，K-Means可以做为其他聚类算法的基础。

基本思想

通过迭代寻找K个簇（Cluster）的一种划分方案，使得聚类结果对应的损失函数最小。其中，损失函数可以定义为各个样本距离所属簇中心点的误差平方和：

$$J(c, \mu)=\sum_{i=1}^{M}{||x_{i}-\mu_{c_{i}}||^{2}}$$

其中 $x_{i}$ 代表第 $i$ 个样本， $c_{i}$ 是 $x_{i}$ 所属的簇， $\mu_{c_{i}}$ 代表簇对应的中心点， $M$ 是样本总数。

主要过程

1. 选定初始簇中心
2. 更新簇中心位置
3. 更新分类归属
4. 重复2、3步到簇中心不在变化

具体过程

KMeans的核心目标是将给定的数据集划分成K个簇（K是超参），并给出每个样本数据对应的中心点。具体步骤非常简单，可以分为4步：

（1）数据预处理。主要是标准化、异常点过滤。

（2）随机选取K个中心，记为 $\mu_{1}^{(0)},\mu_{2}^{(0)},…,\mu_{k}^{(0)}$

（3）定义损失函数： $J(c, \mu)=min\sum_{i=1}^{M}{||x_{i}-\mu_{c_{i}}||^{2}}$

（4）令$t=0,1,2,…$ 为迭代步数，重复如下过程直到 J 收敛：

• 对于每一个样本 $x_{i}$ ，将其分配到距离最近的中心

$$c_{i}^{t} <—argmin_{k}{||x_{i}-\mu_{k}^{t}||^{2}}$$

• 对于每一个类中心k，重新计算该类的中心

$$\mu_{k}^{(t+1)} <—argmin_{\mu}\sum_{i:c_{i}^{t}=k}^{b}{||x_{i}-\mu||^{2}}$$

KMeans最核心的部分就是先固定中心点，调整每个样本所属的类别来减少 J ；再固定每个样本的类别，调整中心点继续减小J 。两个过程交替循环， J 单调递减直到最（极）小值，中心点和样本划分的类别同时收敛。

优缺点

KMenas的优点：

• 高效可伸缩，计算复杂度 为O(NKt)接近于线性（N是数据量，K是聚类总数，t是迭代轮数）。
• 收敛速度快，原理相对通俗易懂，可解释性强。

KMeans也有一些明显的缺点：

• 受初始值和异常点影响，聚类结果可能不是全局最优而是局部最优。
• K是超参数，一般需要按经验选择。
• 样本点只能划分到单一的类中。
• 不适合圆形数据集的分类（非凸数据集）。

  应用

  图像压缩：图像矢量量化。

  对颜色进行聚类，若原图256*256，每个像素用24个比特的RGB表示。若经过聚类颜色之后剩下64种颜色，只用6比特表示颜色，压缩率为$\frac{6}{24}\times 100\%$。

  优化

1. 数据预处理：归一化和异常点过滤

   KMeans本质上是一种基于欧式距离度量的数据划分方法，均值和方差大的维度将对数据的聚类结果产生决定性影响。所以在聚类前对数据（具体的说是每一个维度的特征）做归一化和单位统一至关重要。此外，异常值会对均值计算产生较大影响，导致中心偏移，这些噪声点最好能提前过滤。

2. 合理选择K值

   K值的选择一般基于实验和多次实验结果。例如采用手肘法，尝试不同K值并将对应的损失函数画成折线。手肘法认为图上的拐点就是K的最佳值。

   为了将找寻最佳K值的过程自动化，研究人员提出了Gap Statistic方法。它的有点是我们不再需要肉眼判断，只需要找到最大的Gap Statistic对应的K即可。

   沿用第一节中损失函数记为 $D_{k}$ ，当分为K类时，Gap Statistic定义为： $Gap(k)=E(logD_{k})-logD_{k}$ 。 $E(logD_{k})$ 是 $logD_{k}$ 的期望，一般由蒙特卡洛模拟产生。我们在样本所在的区域内按照均匀分布随机地产生和原始样本数一样多的随机样本，并对这个随机样本做KMeans，得到一个 $D_{k}$ ，重复多次就可以计算出 $E(logD_{k})$ 的近似值。

   $Gap(K)$ 的物理含义是随机样本的损失与实际样本的损失之差。$Gap$越大说明聚类的效果越好。一种极端情况是，随着K的变化 $Gap(K)$ 几乎维持一条直线保持不变。说明这些样本间没有明显的类别关系，数据分布几乎和均匀分布一致，近似随机。此时做聚类没有意义。

3. 改进初始值的选择

   之前我们采取随机选择K个中心的做法，可能导致不同的中心点距离很近，就需要更多的迭代次数才能收敛。如果在选择初始中心点时能让不同的中心尽可能远离，效果往往更好。这类算法中，以K-Means++算法最具影响力。

4. 采用核函数

   主要思想是通过一个非线性映射，将输入空间中的数据点映射到高位的特征空间中，并在新的空间进行聚类。非线性映射增加了数据点线性可分的概率（与SVM中使用核函数思想类似）对于非凸的数据分布可以达到更为准确的聚类结果。

SVM

简介

支持向量机（support vector machines, SVM）是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机；SVM还包括核技巧，这使它成为实质上的非线性分类器。SVM的的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。属于有监督学习。

研究对线性二分类问题的凸优化问题的表示，以及支持向量机的求解。

原理

SVM学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。如下图所示， $\boldsymbol{w}\cdot x+b=0$ 即为分离超平面，对于线性可分的数据集来说，这样的超平面有无穷多个（即感知机），但是几何间隔最大的分离超平面却是唯一的。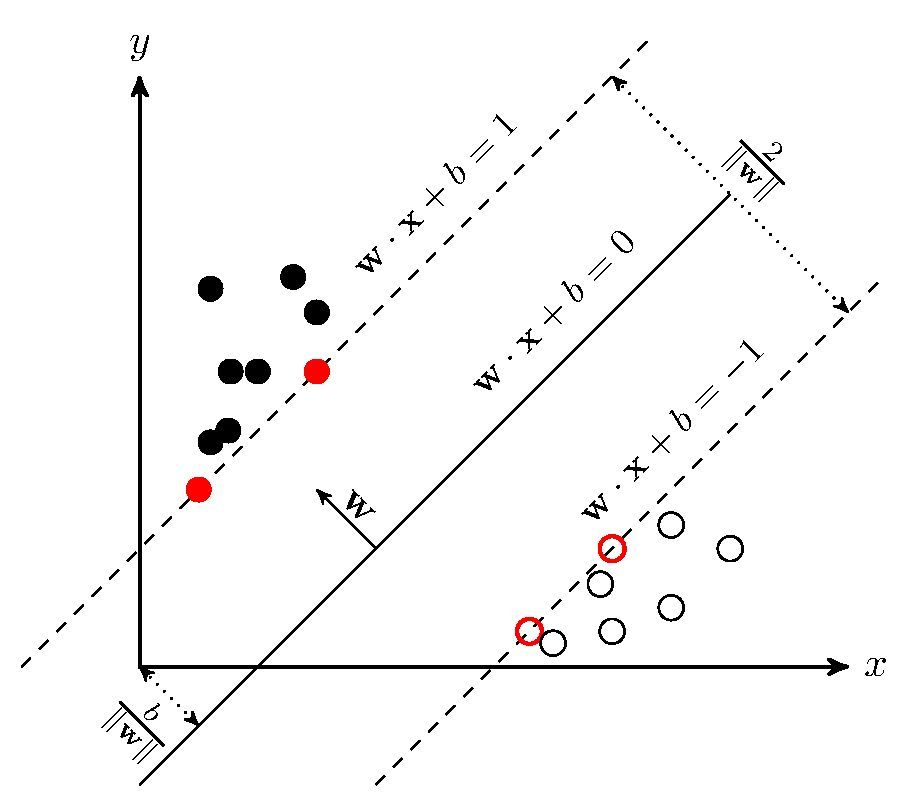

$$w=[w1,w2]\quad x=[x,y]^T$$

点到超平面的距离是

$$d=\frac{|xX_0+b|}{||w||}$$

若$X_0$为支持向量，

$$d=\frac{1}{||w||}$$

用a缩放w和b，$(w,b)\rightarrow(aw,ab)$

当$|wx_0+b|=1$，$x_0$是支持向量。

当$|wx_0+b|>1$，$x_0$非支持向量。

支持向量机的求解

支持向量机求解是一个凸问题，存在唯一一个全局极值。

凸问题总能找到高效快速的算法来解决。

• 拉格朗日乘子法求解
• 用现成数学包求解

  决策树

  决策树是一种十分常用的分类方法，需要监管学习。

  概念

  熵：表示信息的不确定性，即混乱程度。 $$H(D)=-\sum_{i=1}^N p_ilog_2p_i$$ $p_i$表示取到某个信息元素D的概率。

信息增益：表示得知特征A的信息而使得类X得信息不确定性减少得程度。
若用g(D,A)表示特征A对训练数据集D得信息增益，则有：

$$g(D,A)=H(D)-H(D|A)$$

D|A表示加入A特征之后的训练集D。

条件熵：假设在特征A上有m个分支节点，其中$D_i$表示特征A得第i个分支得节点的数据，则

$$H(D|A)=\sum_{i=1}^m\frac{|D_i|}{|D|}H(D_i)$$

即，特征A的分支节点的熵的加权和。

训练期望

• 希望随着树深度的增加，节点的熵迅速的降低。
• 得到一个高度最矮的决策树。
• 到叶子节点的熵值为0，此时叶子节点为纯节点，即每个叶子节点中的实例都属于同一类。

  决策树的构造

  计算所有属性的信息增益，选择当前信息增益最大的特征进行划分。

  改进算法

  CART算法。

  CNN

  卷积神经网络（Convolutional Neural Networks）是一种深度学习模型或类似于人工神经网络的多层感知器，常用来分析视觉图像。

全连神经网络数量太庞大，不适合处理图像，因此需要通过CNN局部感知。
CNN特点：

• 局部感知
• 参数共享
• 多卷积核

• 池化处理

  最大池化、平均池化

• 多层结构

  层数越多，学到的特征越全局化

卷积计算，使用哈达玛积。

步长：滑动的长度

窄卷积和宽卷积：对图像边缘的处理，是否扩充图片边缘。

2023.3.18

图像语义分割

概念：对图像中的每个像素进行分类。

任务：识别图像中存在的内容及位置。

代价函数

用$J(\theta_1)$表示$h_{\theta}(x)$的代价函数。

$$J(\theta_1)=\frac{1}{2m}\sum(h_\theta(x^{(i)})-y^{(i)})^2$$

梯度下降法

$$\theta_j=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1) \space\space(for\space j=0\space and\space j=1)$$

$\alpha$称为学习率，学习率太大，会导致发散，学习率太小，会导致收敛过慢。
如何找到合适的学习率？
画出$min\space J(\theta)-No.of\space iteration$图像，判断算法是否已经收敛，挥着通过自动收敛测试判断。如果函数递增，则说明没有收敛，需要使用较小的学习率。最开始的时候可以每隔十倍取一次值尝试。
convex function 凸函数
Feature Scaling：通过放缩特征数据的范围一致，使得梯度下降法运行效果更加丝滑。
Mean normalization（均值归一化）：通过平移和放缩，使得特征数据的样本中心接近。
可以通过简单的特征变换，拟合不同的函数。

正规方程法

正规方程法求$\Theta$推导：
设样本特征数为n，样本个数为m，则设$X$为样本构成的$n\times m$的矩阵，$Y_{m\times 1}$为真实预测值，$\Theta_{n\times 1}$为待求参数值，则价值函数的矩阵形式为：

$$J(\Theta)=(X\Theta -Y)^T(X\Theta -Y)$$

由微分知识可知，当任意的$\theta_i$满足

$$\frac{\partial}{\partial\theta_i}J(\Theta)=0$$

时，存在极值，于是对于每个$\theta_i$，求$J(\Theta)$的偏导等于0。化简，得到：

$$J(\Theta)=\Theta^T X^TX\Theta-2Y^TX\Theta$$

考虑在$A_{1\times n}\Theta_{n\times 1}$中，对每一个$\theta_i$求导，得到极值条件：

$$A^T=0$$

考虑在$\Theta_{n\times 1}^T A_{n\times n}\Theta_{n\times 1}$中，对每一个$\theta_i$求导，得到极值条件：

$$\frac{\partial}{\partial \theta_i}(\Theta_{n\times 1}^T A_{n\times n}\Theta_{n\times 1})=\frac{\partial}{\partial \theta_i}(\Theta^Ta_{xi}+a_{ix}\Theta-\theta_i^2aii)=2a_{ix}\theta_i$$

因此通过求导和重新排列，· 得到$J(\Theta)$的极值条件：

$$2X^TX\Theta -2X^TY=0$$

即

$$\Theta=(X^TX)^{-1}X^TY$$

线性代数中，可以通过正规方程法，直接求使得代价函数最小的$\Theta$，但是由于正规方程法是$O(n^3)$复杂度，在数据量很大时，只能使用梯度下降法。