形式语言与自动机

第一章

集合与关系

图

证明技术

第二章

定义

• 形式语言——字符串
• 自动机——字符串的识别系统
  • 外部激励输入+状态转移

语言	自动机
非限定语言	图灵机
上下文有关语言	线性有界自动机
上下文无关语言	下推式存贮自动机
正则语言	有限自动机

一定类型的自动机和某种类型的语言有等价性。

字母表

常用T，用$\Sigma$表示，是字符的有线集合。

字符串

字符串：由字母表T中的字符构成的有线序列。

句子：合法的字符串。

长度：字符串所包含字符的个数。

空串：没有任何字符的字符串，记为$\varepsilon$。

约定小写字母$a,b,c,d$表示单个字符，$t,u,v,ω,x,y,z$表示字符串，$a^n$表示n个a的字符串。

连接：$ω_1 ω_2$表示把两个字符串连接在一起。

字符串的逆：表示为$\widetilde{ω}$，当$ω=b_1 b_2···b_k$，则$\widetilde{ω}=b_k···b_2 b_1$，且$\widetilde{\varepsilon}=\varepsilon$。

前缀：$ω_{1}$是$ω_{1}ω_{2}$的前缀。

后缀：$ω_{2}$是$ω_{1}ω_{2}$的后缀。

子串：$ω_{2}$是$ω_{1}ω_{2}ω_{3}$的子串。

幂运算和闭包运算

$T^*$（克林闭包）:字母表上所有字符串和空串的集合。

$T^+$（正闭包）:不包含空串。

$T^{+}=T^{*}-\left\{\varepsilon\right\}$

语言

任何集合$L \in T^*$，L为一个语言。

对于集合的运算可以运用在语言上。

语言的积：类似于集合中的笛卡尔积，$L_{1}·L_{2}$ 或 $L_{1}L_{2}$ 是由 $L_{1}$ 和 $L_{2}$ 中字符串的连接构成的字符串集合。

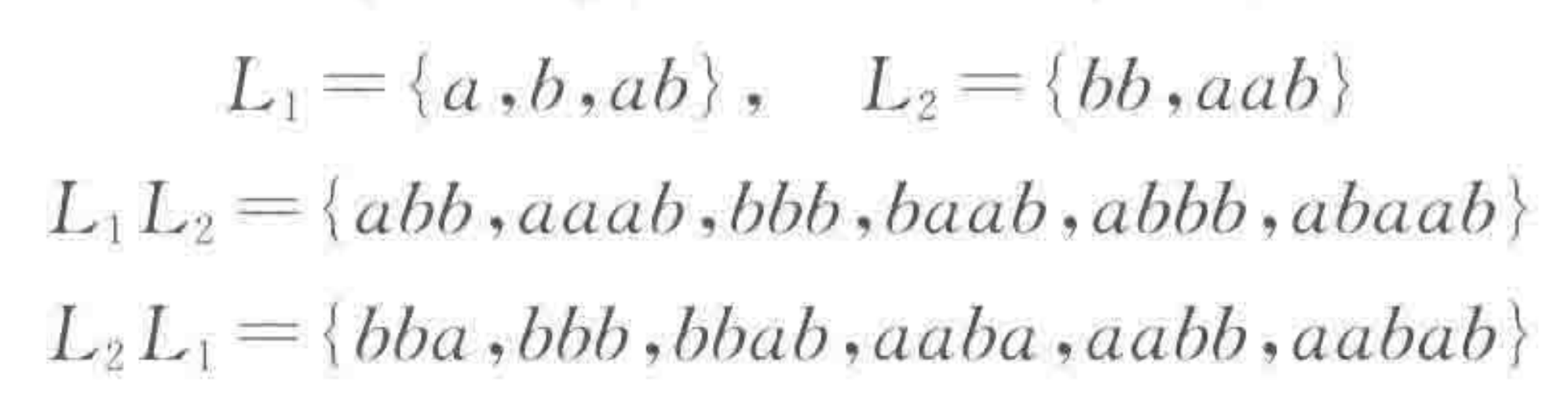
$L_{1}L_{2} \neq L_{2}L_{1}$，语言的积运算是不可交换的。

语言的闭包：

元语言

描述语言的语言，例如各种各样的程序设计语言。当需要讨论该语言本身时，被讨论的语言叫对象语言。

BNF（巴斯克范式）

对各种语言，相当于一个元语言，常用来讨论各种程序设计语言。

文法

产生语言的语言。

Chomsky文法体系

• 非终结符集合N
• 终结符集合T
• 起始符号S
• 生成式集合P

文法的生成式集合例子：

• I->L
• I->IL
• I->ID
• L->a|b|……|z
• D->0|1|……|9

推导与句型

推导序列：直接推导的序列，生成式只用一次。

• 推导一步：直接推导；推到两步及以上：间接推导。

句型：推导每一步都产生的一个字符串。

句子

句型包含句子。句子由终结符构成，没有了变化的可能性。
由文法G产生的语言几位L(G)

文法体系分类

• 0型

  没有任何限制。

• 1型

  生成式形式：
  $\alpha\rightarrow \beta$，其中$|\alpha| \leq |\beta|$，且$\alpha ,\beta \in (N\cup T)^+$，且$\alpha$至少含有一个非终结符。

  上下文有关文法，线性有限自动机，越推越长或相等。

• 2型

  生成式形式：$A\rightarrow \alpha,A\in N$且$a\in (N\cup T)^*$

  上下文无关文法，下推自动机，生成式左边都是单个非终结符。

• 3型

  生成式形式（右线性文法）：$A\rightarrow wB$或$A\rightarrow w$，$A,B\in N$,$w\in T^*$

  正则文法，左（右）线性文法，只用一个非终结符在产生式结果的最左（右）边。

3型文法属于2型文法，2型文法属于1型文法

1型文法中不允许 $A\rightarrow\varepsilon$ 的生成式存在，所以有 $A\rightarrow\varepsilon$ 的2型或3型文法不能属于1型文法

例题：

找出右线性文法，能构成具有奇数个a和奇数个b的所有由a和b组成的字符串。

$$\begin{aligned} G&=(N,T,P,S)\\ N&=\{S,A\}\\ T&=\{a,b\}\\ P&:\\ &S\rightarrow ab|ba|aaS|bbS|abA|baA\\ &A\rightarrow \varepsilon |aaA|bbA|abS|baS\\ \end{aligned}$$

思路：

• 起始符S可以到ab或者ba。
• 当在句型中增加偶数个a或偶数个b，一定符合题目要求，推出$S\rightarrow aaS|bbS$。
• 单独的非终结符S不能有$S\rightarrow abS|baS$，应为会导致ab的奇偶状态不确定。因此引入非终结符A，推出$A\rightarrow abA|baA$。
• A中应该确保只能推出偶数个的ab构成的字符串，因此推出$A\rightarrow aaA|bbA|abS|baS|\varepsilon$满足题意。
• 大致上感觉S代表奇数状态，A代表偶数状态。

  第三章

  有限自动机

  状态：离散的将事物区分开的一种标识。
  不一定只有一个终止状态

有限自动机的五要素：

• 有限状态集
• 有限输入符号集
• 转移函数
• 初始状态
• 终止状态集

确定的有限自动机（DFA）

$$M=(Q,T,\delta,q_0,F)$$

Q：有限的状态集合。
T：有限的输入字母表。
$\delta$：转换函数，是从$Q\times T$到$Q$的映射。
当输入的是一个字符串时，转换函数用$\delta’$表示，$\delta’$是从$Q\times T^{*}$到$Q$的映射，将字符串一个一个拆分，再将这些行为一步步串起来
$\delta’(q,\omega a)=\delta(\delta’(q,\omega),a)$

$L(M)$表示$M$所接受的语言，表示为
$L(M)=\left\{\omega|\delta’(q_{0},\omega) \in F \right\}$

对任意字符串$w\in T^*$，$\delta’(q,w)$表示DFA在状态q，输入字符串w之后的状态。

$$(q,aw)|——(q_1,w)$$

格局

用于描述瞬时状态。格局的状态是无限的。
若某个字符串$\omega$可以从初始格局开始，经过一系列格局变换最后到达接受格局$(q_{n},\omega)$，则表示该字符串$\omega$可被确定的有线自动机接受。

例：

对于$L=a^nb$的自动机M，用格局识别$w=aab$。

$$(q_0,aab)|——(q_0,ab)|——(q_0,b)|——(q_1,\epsilon)$$

不确定的有限自动机（NFA）

下一个状态可能存在若干选择

$$M=(Q,T,\delta,q_0,F)$$

$\delta$是从$Q\times T$到$2^Q$的映射.

DFA是NFA的特例。

DFA与NFA等效

NFA与DFA具有等价性：一个能被NFA接收的语言，一定存在一个DFA能够接收。

NFA转化DFA

利用队列，从$q_0$开始，不断将NFA中的状态和状态集合写入转移表中，用NFA中状态的子集作为一个新的状态，转化成DFA。

有ε转换的不确定的有限状态自动机

当输入空串ε时，也能引起状态的转换
有ε转换的NFA和无ε转换的NFA，区别仅在于转换函数δ的不同

$$M=(Q,T,\delta,q_0,F)$$

其中$δ$是从$Q×(T\bigcup\left\{ε\right\})$到$2^{Q}$的映射

在输入字符串时，它的转换函数$δ’$是从$Q×T^{*}$到$2^{Q}$的映射
在构造$δ’$时，需要找到从已给状态$q$，仅用$ε$转换（经过长度为0的路径）便可达的状态集合P
用 $ε-closure(q)$ 表示P，称为q的 $ε-$闭包

对于一个状态子集$I$：

$$ε-closure(I)=\bigcup\limits_{q\in I}ε-closure(q)$$

对于一个状态子集$I_{a}$，任意$a\in T$，定义如下：（其中$P$是$I$中状态经过一条标$a$的边可到达的状态集合）

$$I_{a}=ε-closure(P)$$

有ε转换NFA和无ε转换NFA的等效

有ε转换NFA，无ε转换NFA，DFA三者等效

有ε转换NFA转换为无ε转换NFA：

1. 构造无ε转换NFA $M_1=(Q,T,\delta_1,q_0,F_1)$
2. $$F_1=\left\{ \begin{array}{rcl} F\bigcup\left\{q_0\right\} & & {当ε-closure(q_0)含F的一个状态}\\ \\ F & & {否则} \end{array} \right.$$
3. $\delta_1(q,a)=\delta’(q,a)$=$ε-closure(\delta(\delta’(q_0,ε),a))$

正则式

字母表T上的递归定义：

1. $ε$和$\varnothing$都是正则式，分别对应的正则集是$\left\{ε\right\}$和空集$\varnothing$
2. 任意$a\in T$是正则式，分别表示的正则集是$\left\{a\right\}$
3. 若A和B是正则式，分别表示的正则集是L(A)和L(B)，则$(A+B)、(A·B)、(A^)$也是正则式，分别表示的正则集为$L(A)\bigcup L(B)、L(A)L(B)、L(A)^$，星表示闭包。

由右线性文法得到正则式的求解规则R：
设 $x=\alpha x+\beta,\alpha\in T^{},\beta\in(N\bigcup T)^{},x\in N$ ，那么它的解为：$x=\alpha^*\beta$

右线性文法产生的语言是正则集。

正则表达式，正则文法（右线性文法），有限自动机都定义了同一种语言正则语言。

定理：任意右线性文法G定义的语言必然能被一个NFA M所接受。

右线性文法和正则集

右线性文法和正则集等价
一个语言是正则集，当且仅当该语言为右线性语言

右线性语言$L_1$和$L_2$分别由右线性文法$G_1$和$G_2$产生，$G_1=(N_1,T,P_1,S_1)$，$G_2=(N_2,T,P_2,S_2)$，其中$N_1\bigcap N_2=\varnothing$

对于$L_1\bigcup L_2$，设右线性文法$G=(N,T,P,S)$，其中
$N=N_1\bigcup N_2\bigcup \left\{S\right\}$
$S\notin N_1\bigcup N_2$是一个新非终结符
$P=P_1\bigcup P_2\bigcup \left\{S→S_1,S→S_2\right\}$

对于$L_1L_2$，设右线性文法$G=(N,T,P,S)$，其中
$N=N_1\bigcup N_2$
$S=S_1$

对于$L^*$，设有右线性文法$G=(N,T,P,S)$，其中
$N=N_1\bigcup \left\{S\right\}$
$S\notin N_1$，$S$是一个新非终结符
生成式$P$如下：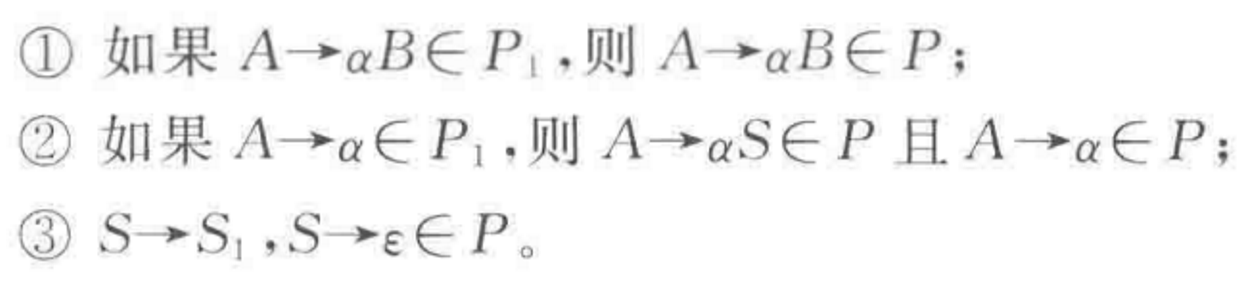

正则表达式和有限自动机

扩充正则式：

由正则式构造有ε转换的不确定的有限自动机：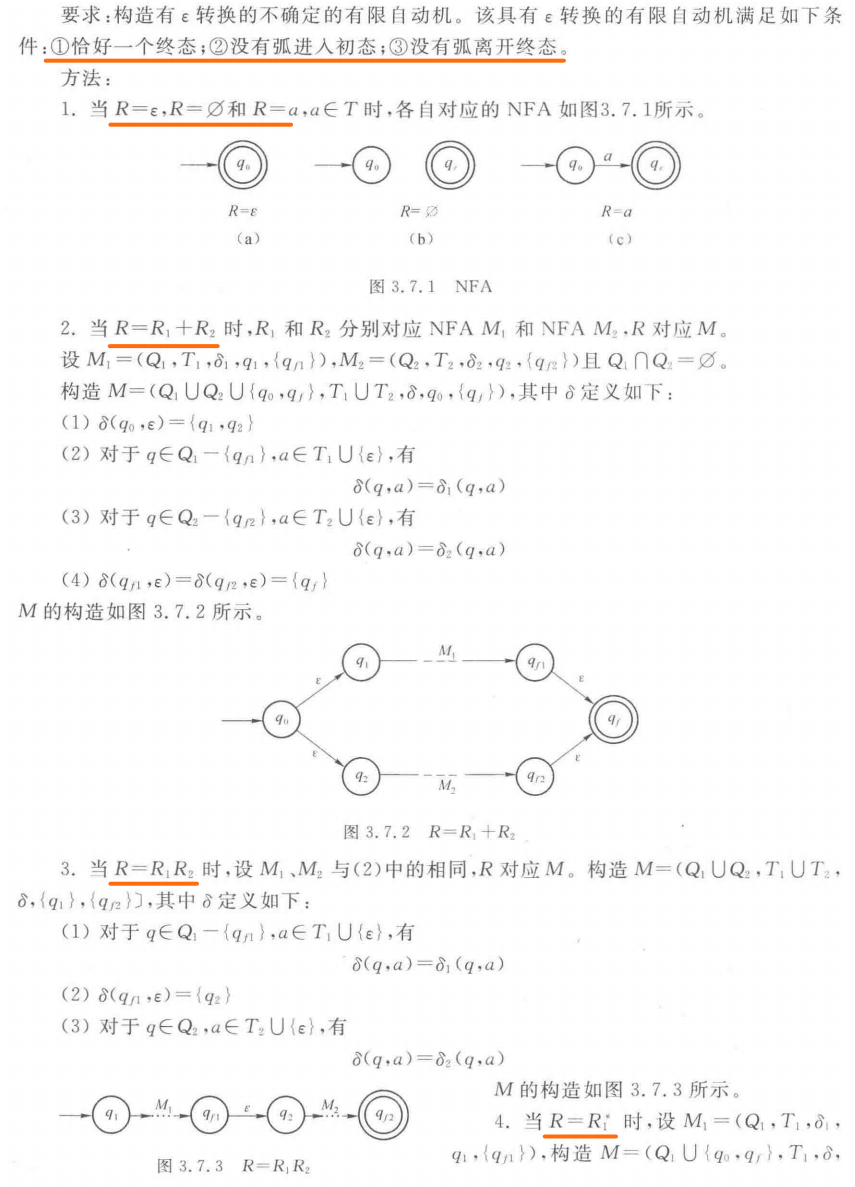

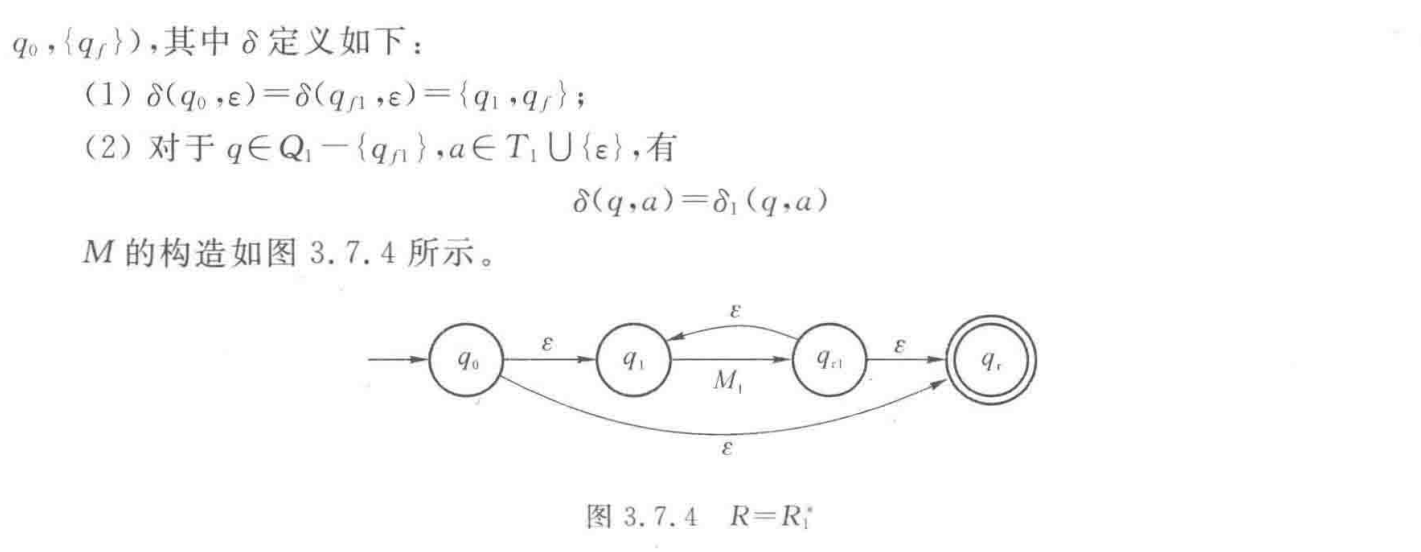
确定的有限自动机构造等价的正则表达式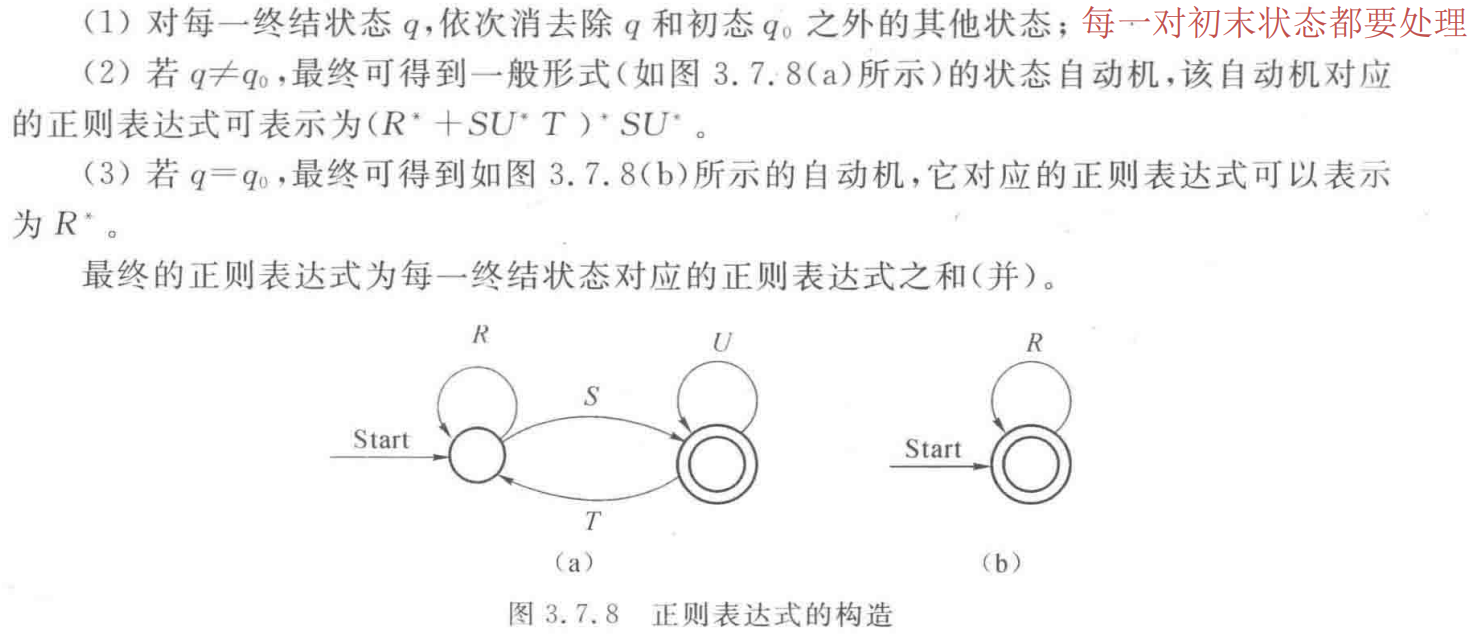

右线性语言和有限自动机

右线性文法$G=(N,T,P,S)$产生的语言$L(G)$，存在一个有限自动机M，使得$L(G)=L(M)$

确定的有线自动机的化简

一个DFA M的最小化，是把M的状态集Q构成一个划分，即任何两个子集（两个划分块）的状态都是可区分的，同一子集（即同一划分块）中的任何两个状态都是等价的。最后每一个子集代表一个状态,并取一个状态名。

计算状态集划分的算法——填表法

泵浦引理

右线性语言的封闭性

$L_1\bigcup L_2:$

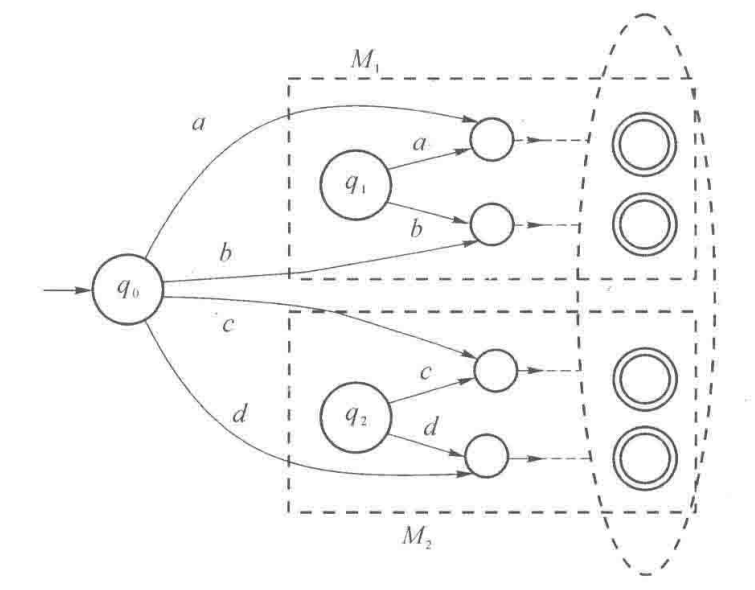
$L_1L_2:$

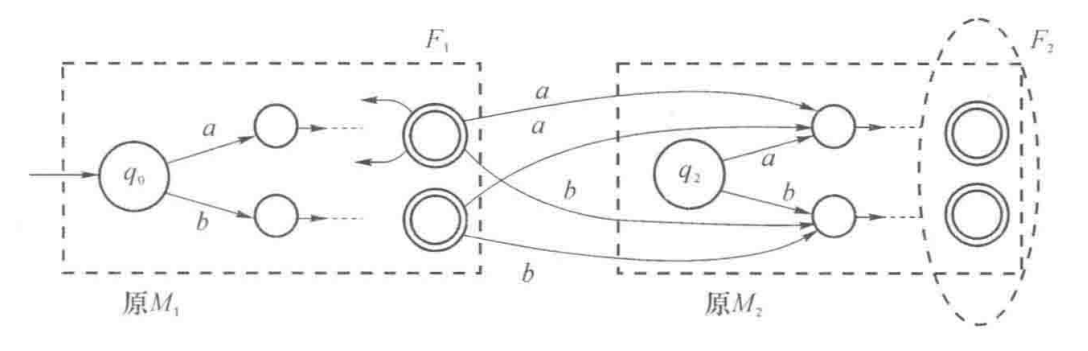
$L^*:$

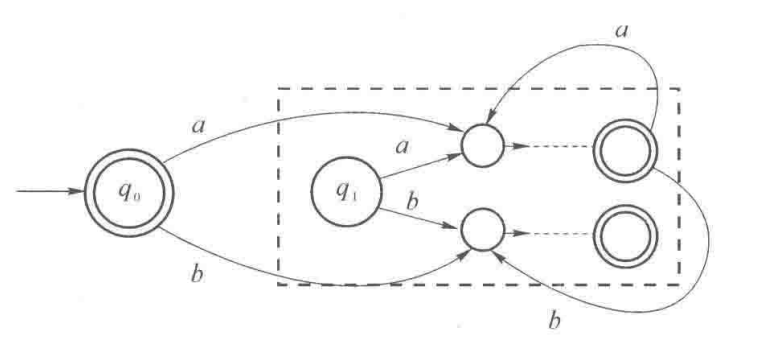
$\overline{L}:$

$L_1\bigcap L_2:$
$L_1\bigcap L_2=\overline{\overline{L_1}\bigcup \overline{L_2}}$

右线性语言对置换是封闭的

米兰机

$$M=(Q,T,R,\delta,g,q_0)$$

• Q：有限状态集合
• T：有限输入字母表
• R：有限输出字母表
• $\delta$：$Q\times T\rightarrow Q$转换函数
• g：$Q\times T\rightarrow R$输出函数
• $q_0$：初始状态

  摩尔机

  $$M=(Q,T,R,\delta,g,q_0)$$
• Q：有限状态集合
• T：有限输入字母表
• R：有限输出字母表
• $\delta$：$Q\times T\rightarrow Q$转换函数
• g：$Q\rightarrow R$输出函数
• $q_0$：初始状态

双向有限自动机

将读头的移动扩展为既能向右移动又能向左移动，那么读入一个字符之后，读头既可右移一格也可左移一格，或者不移动

上下文无关文法与下推自动机

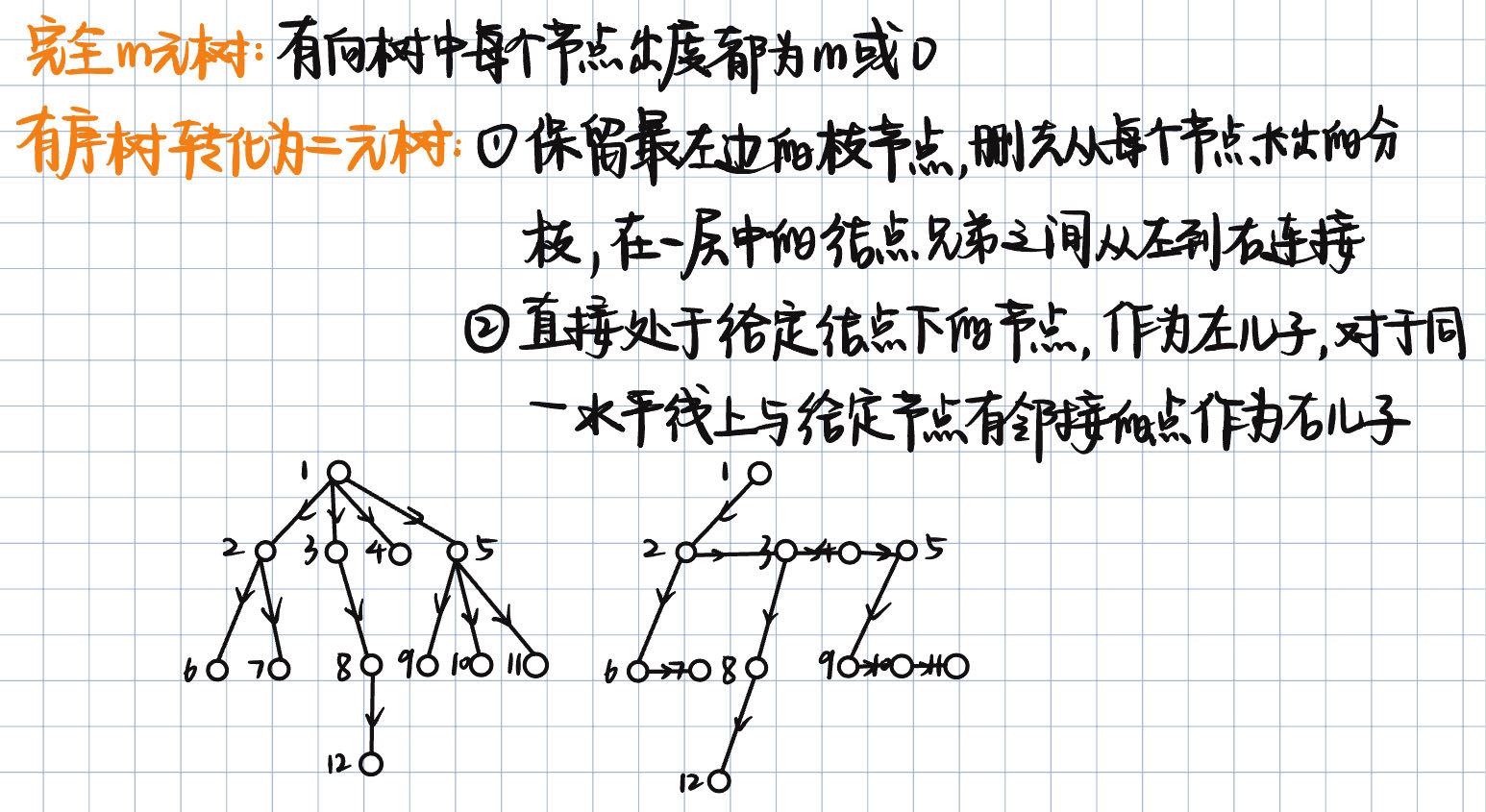
设D是上下文无关文法G=(N,T,P,S)的推导树，是有标记的有序树，且满足

1. D的根节点标记是S；
2. D的直接点的标记是非终结符；
3. D的叶节点标记是终结符或$\epsilon$；
4. 如果标记为A的节点，有直接子孙$X_1,X_2,\dots,X_k$，那么 $$A\rightarrow X_1X_2\dots X_i$$ 是P的一个生成式。

上下文无关文法G是二义的，当且仅当对于句子$w\in L(G)$，存在两颗不同的具有边缘为$w$的推导树。

设上下文无关文法G=(N,T,P,S)

……未完待续♬