计算机组成原理 第二章

第二章：运算方法和运算器

数据与文字的表示方式

真值和机器数

数据表示需要考虑的因素：

1. 数据的类型
2. 可能遇到的数值范围
3. 数值精确度
4. 数据存储和运算的硬件代价

数据的表示格式：

1. 定点格式
2. 浮点格式

真值： 现实中真实的数值
机器数： 计算机中用0和1组合表示的数值
定点数：固定小数点的未至表达数值的机器数

• 定点整数：将小数点固定在机器数的最右侧表达的整数
• 定点小数：将小数点固定在机器数的最左侧表达的小数

浮点数：小数点浮动表达的实数
无符号数：只表达0和正整数的定点整数
有符号数：表达负整数、0和正整数的定点整数

• 符号位需要占用一个位，常用机器的最高位
• 0表示正数，1表示负数
• 具有原码、反码、补码、移码

无符号数与定点数的表示

没有符号位，使用全部字长来表示数值大小
举例：

字长N=8时，编码00000000~11111111
取值范围： 0~255（2⁸-1）

定点表示：约定机器中所有数据的小数点位置是固定不变的。通常将数据表示成纯小数或者纯整数。
定点数x=x₀x₁x₂……x_n表示如下（x₀表示符号位，0正1负）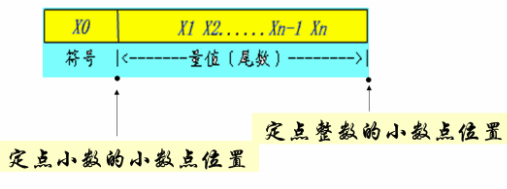

举例：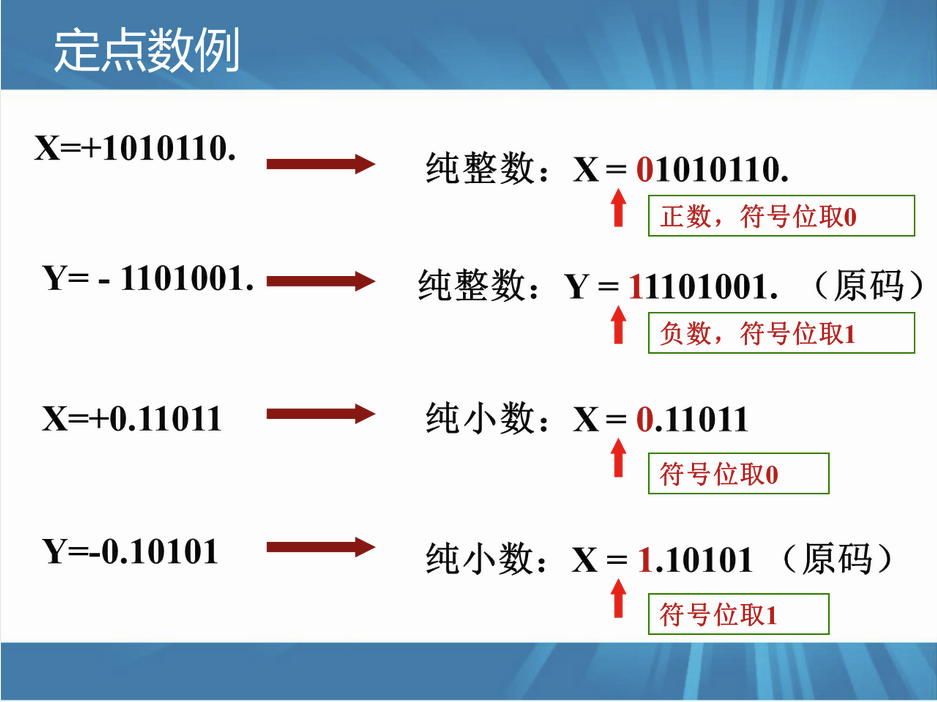

定点小数的取值范围
纯小数的表示范围为：
x₁x₂x₃……x_n各位均为0时最小，各位均为1时最大，x₀为符号位

0 ≤ |x| ≤ 1 - 2^-n

定点整数的表示范围：
纯整数的表示范围为：
x₁x₂x₃……x_n各位均为0时最小，各位均为1时最大，x₀为符号位

0 ≤ |x| ≤ 2ⁿ - 1

目前计算机中多采用定点纯整数表示，因此将定点数的运算简称为整数运算

既然定点数有大小范围，那我们如何用定点数表示非常大的数和非常小的数呢？
我们可以引入比例因子：

优点:方法简单，计算方便
缺点:表示数字的范围有限，要表示大或小的数字必须使用很多比特
大数量级数据的表示：

• 定点计算机间接表示:运算前按一定的固定比例(比例因子)缩放
• 运算后再用幂方式

浮点数的表示方法

把一个数的有效数字和数的范围在计算机的一个存储单元中分别予以表示。
数的小数点位置随比例因子的不同而在一定范围内自由移动。

一个十进制数N可以写成：

N = 10^e×M

则，一个R进制数N可写成：

N = R^e× M

M：尾数
e：指数
R：基数

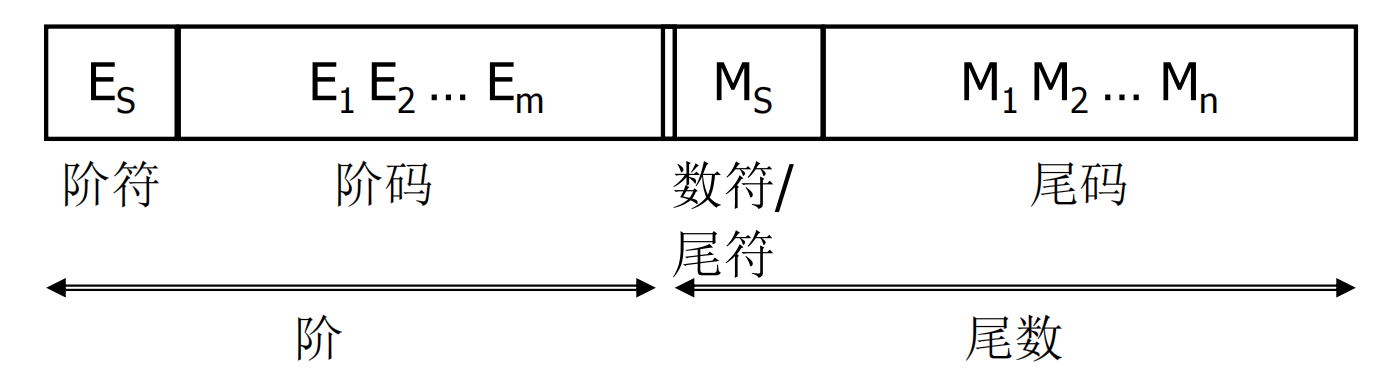
阶码和尾数
阶码：表达指数部分。用整数形式表示，指明小数点在数据中的位置，决定浮点数的表示范围。
尾数：用定点小数表示，给出有效数字的位数，决定了浮点数的表示精度。

十进制数串的表示方法（非压缩型
）：

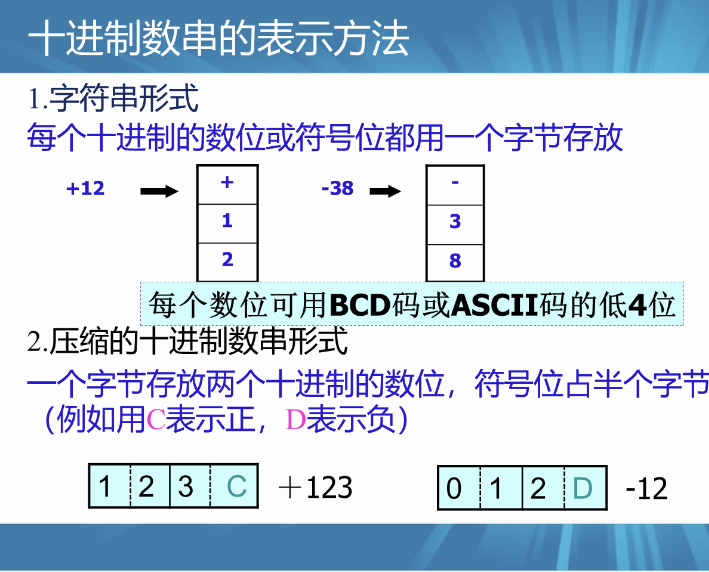
BCD码

二十进制编码部分方案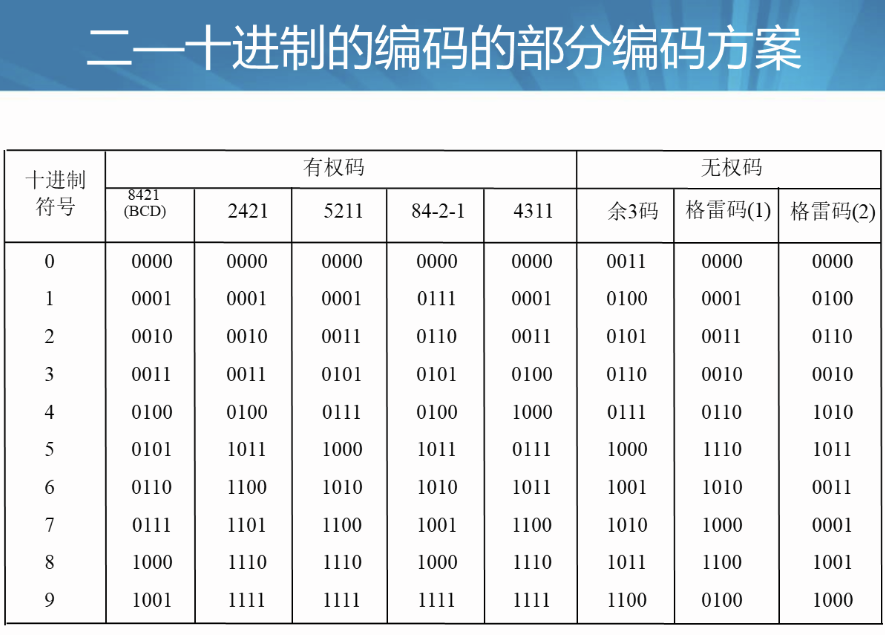

二十进制有权码：
对于有权码，将每位的数码与相应的位权相乘，再求和，就可以得到它所代表的十进制数值。
8421码实现加减运算时的修正规则：

1. 未超出9（1001），不进行修正
2. 超出9（1001），不超过16（10000），加6修正，使它向高一组产生进位，省去最高位。
3. 超出16（10000），加6修正。

余三码
余三码是在8421码的基础上，把每个代码都加上0011而形成的。
普通8421码的加法器仍能为余三码加法器直接利用，具体规则如下：

1. 若两个十进制数的余三码相加，如果结果不产生进位，则从所得和值减去0011，便得十进制位和的余三码。
2. 若两个十进制的余三码相加，如果结果有进位，则其进位正确，但仍需将所得值加上0011.才求的十进制和的余三码。

格雷码
格雷码的编码规则是使相邻的两个代码，只有一个二进制的状态不同，其余三个二进制位必须有相同状态。
优点：从一个编码变到下一个相邻编码时，只有一个位的状态发生变化，有利于保证代码变换的连续性。在模拟/数字转换和产生节拍电位等应用场合特别有用。

数的机器码表示

把符号位和数值位一起编码来表示相应的数。

• 原码
• 补码
• 反码
• 移码

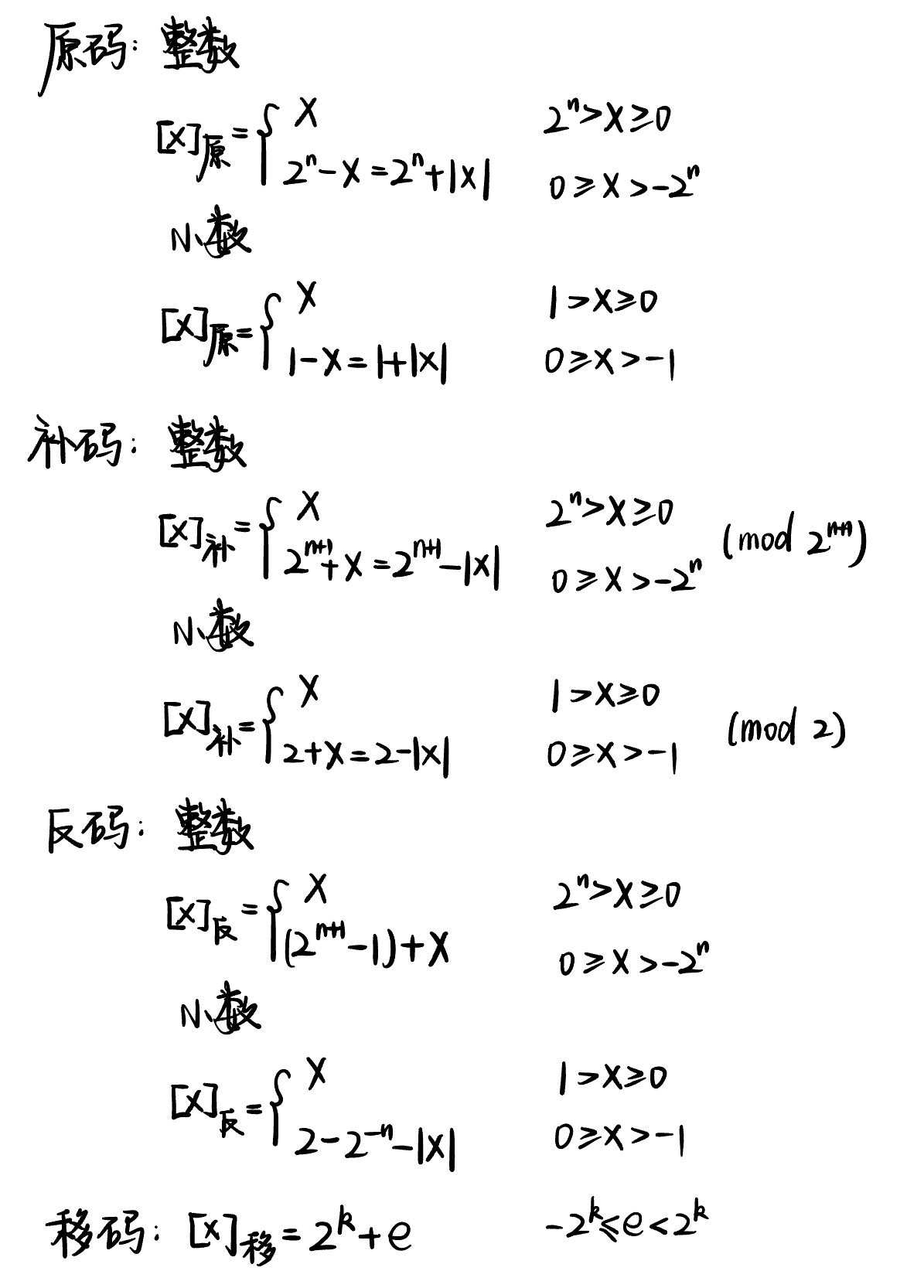
原码

定点整数的原码形式为x₀x₁x₂……x_n（x₀为符号位）
举例：
定点小数的原码形式为x₀x₁x₂……x_n（x₀为符号位）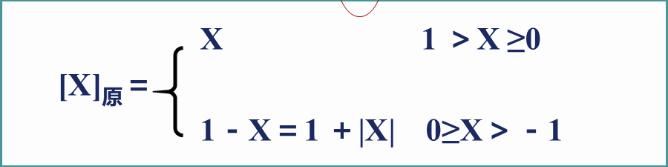

举例：

原码的表示范围：
原码总结

1. 原码为符号位加上数的绝对值，0正1负。
2. 原码0有两个编码，+0和-0编码不同
3. 原码表示简单，易于同真值之间进行转换。
4. 原码乘除运算规则简单
5. 原码加减运算负责
   当两数相加时，同号则相加；如果是异号则相减。而在进行减法运算时，还要比较绝对值的大小，然后大数减去小数，最后还要给结果选择符号。

补码

模的概念：
计算机中运算器、寄存器、计数器都有一定的位数，不可能容纳无限大的任意数。当运算结果超出实际的最大表示范围，就会发生溢出，此时所产生的溢出量就是模(module)。
模定义为一个计量器的容量。如：一个4位的计数器它的计数值为0~15。当计数器计满15之后再加1，这个计数器就发生溢出，其溢出量为16，模等于16。定点小数的溢出量为2，即以2为模；
一个字长为n+1位的定点整数的溢出量为2ⁿ⁺¹,即以2ⁿ⁺¹为模。

定点整数的补码形式：x₀x₁x₂……x_n（x₀为符号位）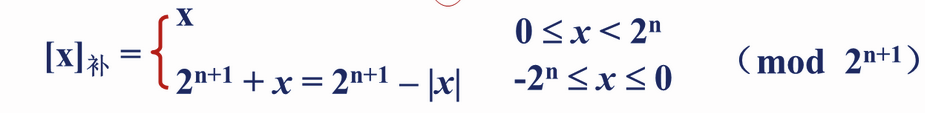

举例：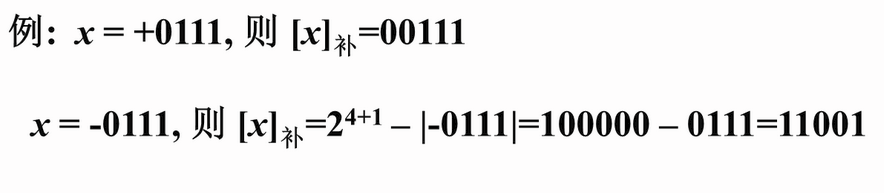

定点小数的补码形式：

补码与真值：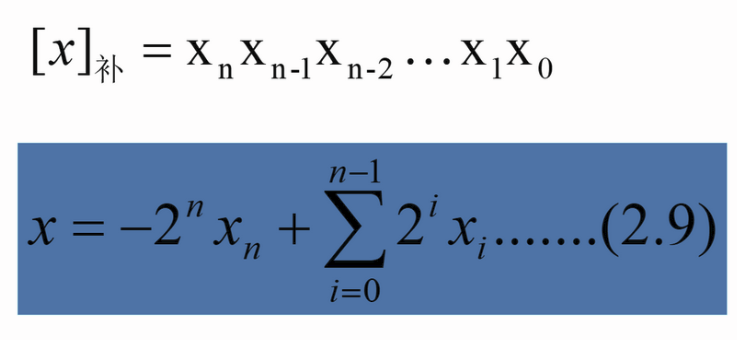


举例：

定点整数的补码表示：
有符号整数在计算机中默认采用补码。

• 最高位表示符号，0正1负
• 正数补码：直接表示数值大小（=原码=无符号数）
• 负数补码：将对应的正数原码取反加1

举例：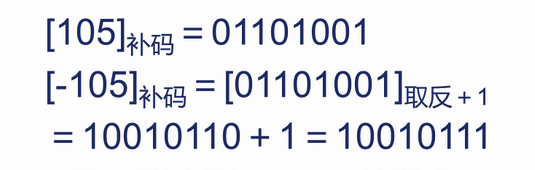

负数求补:
负数真值“取反加一”得到机器数补码
负数补码“取反加一”得到负数真值

负数求补运算，等效于用带借位的0做减法

补码的特点

1. 补码最高一位为符号位，0正1负
2. 补码零具有唯一编码
3. 补码的加减运算规则简单
   最高位参与运算，与其他位一样对待

反码

反码：二进制的各位数码0变1，1变0
有符号整数的反码：

1. 最高位表示符号，0正1负
2. 正数反码：直接表示数值大小（=原码=补码）
3. 负数反码：将原码符号位不变其他位取反

例题：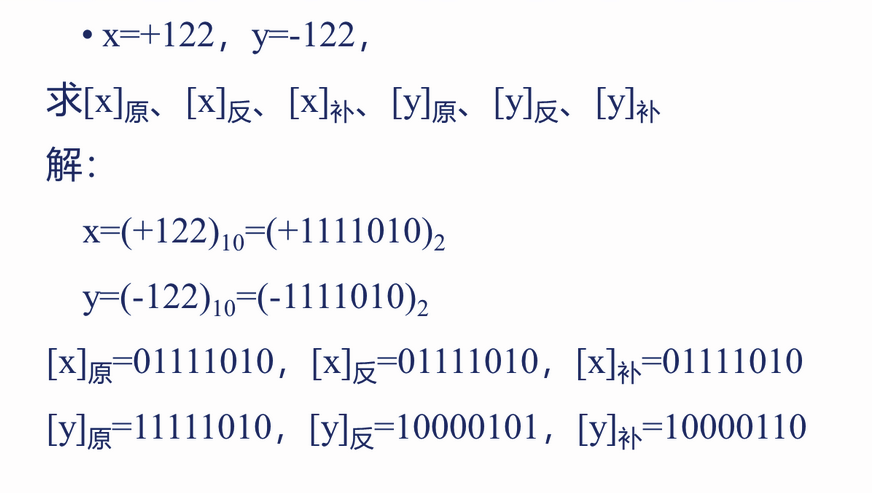

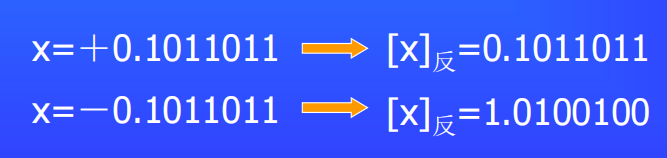
反码和补码的关系：
同一个负数的补码和反码只在最低有效比特上差1
$[X]_{补}=[X]_{反}+2^{-n}$

机器码右移位

原则：移位时应保持移位前后机器码的对应关系与真值移位相同

• 每右移一位，真值的绝对值减为1/2

原码:符号位固定在最高位，左边空出的数值位补0
补位和反码:符号位固定在最高位，左边空出的数值位补符号位

例如：$[X]_{补}=1.01001110$
=> $[X/2]_{补}=1.10100111$

补码位数扩展

原则：扩展后真值不变

• 定点纯整数
  补码：符号位固定在最高位，左边空出的数值补符号位
• 定点纯小数
  补码：右边空出的数值位补0

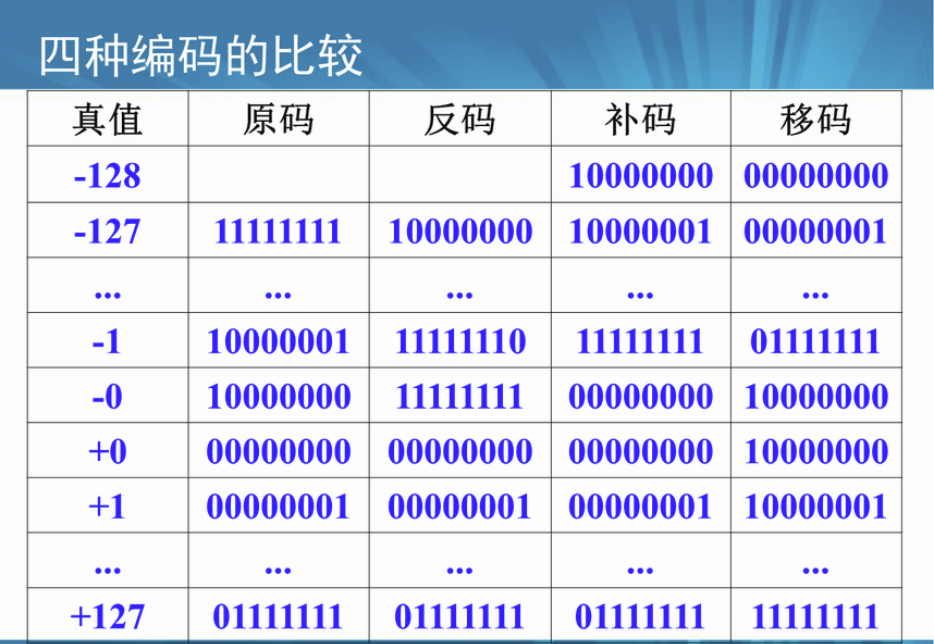
移码

移码符号位表示的规律与原码、补码、反码相反
移码与补码仅差符号位

定点加法、减法运算

补码加法

补码加法的公式为：

在模2ⁿ⁺¹意义下，任意两数的补码之和等于改两数之和的补码。

例题：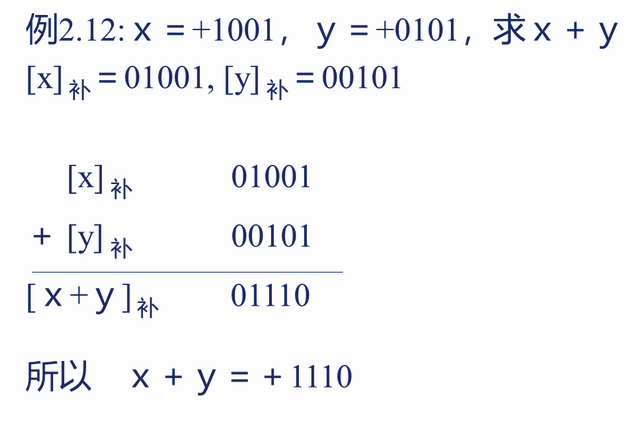

补码加法的特点：

1. 符号位要作为数的一部分一起参加运算
2. 要在模2ⁿ⁺¹的意义下相加，即超过模的进位要丢掉

补码减法

补码减法公式是：

溢出概念与检验方法

在定点整数机器中，n+1位数的表示范围为$-2^{n}<X<2^{n+1}-1$
在定点小数机器中，n+1位数的表示范围为$-1<X<1-2^{-n}$
在运算过程中如出现大于绝对值的现象，称为溢出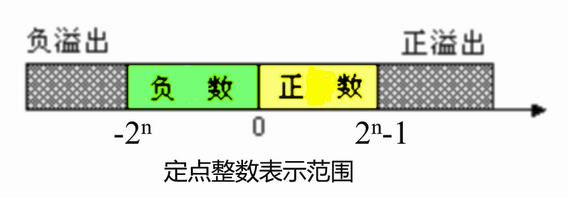

两个正数相加，结果大于机器所能表示的最大正数，称为正溢
两个负数相加，结果小于机器所能表示的最小负数，称为负溢

例题：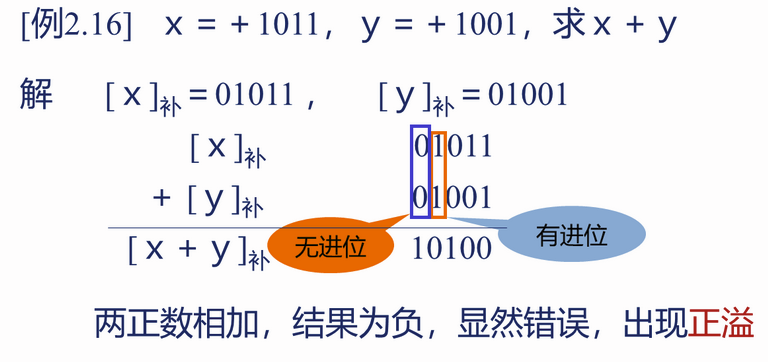

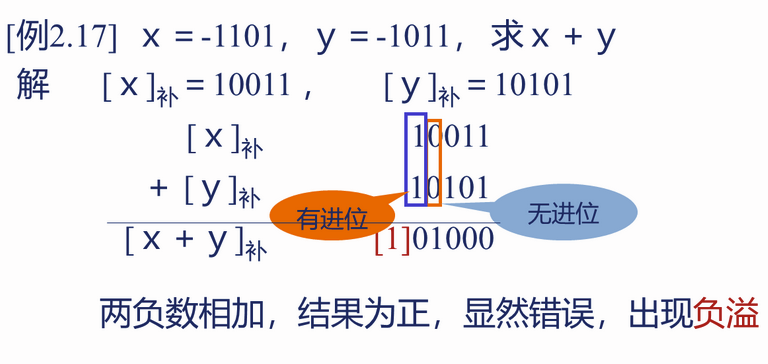
溢出原因分析：
分析可知，当最高有效数值位的运算进位与符号位的运算进位不一致时，将产生运算溢出

溢出检测方法

单符号位法

当最高有效位有进位而符号位无进位时，产生正溢
当最高有效位无进位而符号位有进位时，产生负溢
溢出检测逻辑表达式：$V=C_{f}\oplus C_{0}$

变形补码法

双符号位法，称为“变形补码”或 模2ⁿ⁺²补码
可使模2ⁿ⁺²补码所能表示的数的范围扩大一倍
变形补码定义为：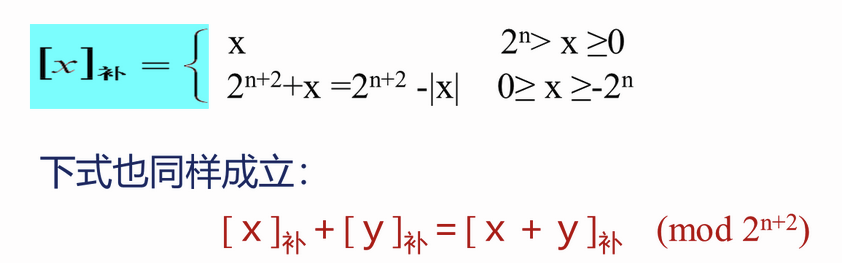

计算时：

1. 两个符号位都看作数码一样参加运算，两数进行2ⁿ⁺²为模的加法，即最高符号位上产生进位要丢掉 ，模2ⁿ⁺²补码相加的结果，不论谥出与否，最高符号位始终指示正确的符号。
2. 当以变形补码运算，运算结果的二符号位相异时，表示溢出，溢出类型和最高符号位有关；相同时，表示未溢出，没有发生溢出的情况下，正数符号位为00，负数符号位为11。
3. 溢出逻辑表达式为$V=S_{f1}⊕S_{f2}$,其中$S_{f1}$和$S_{f2}$分别为最高符号位和第二符号位。此逻辑表达式可用异或门实现。

例题：

基本二进制加法 / 减法器

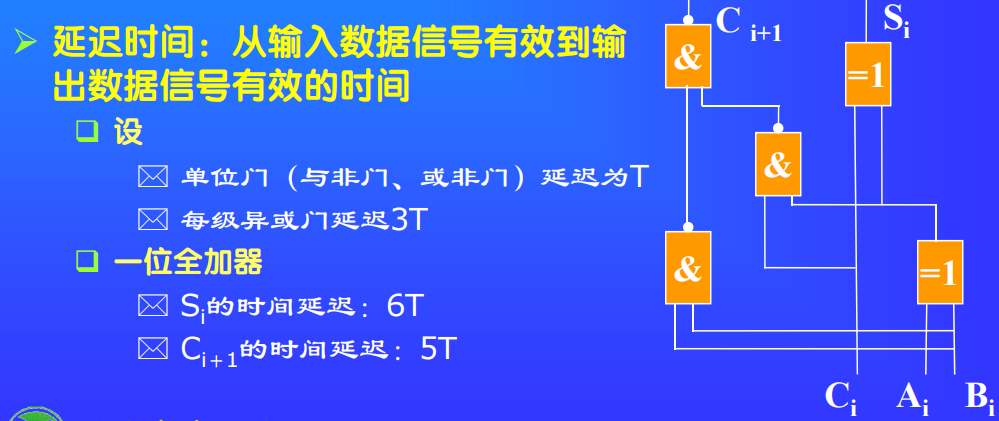
一位全加器

两个二进制数字A_i，B_i和一个进位输入C_i相加，产生一个和输出S_i，以及一个进位输出C_i+1

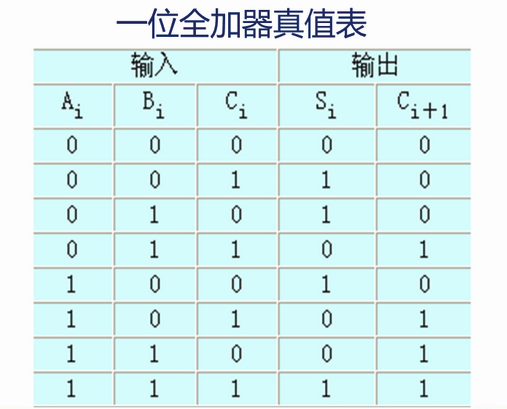
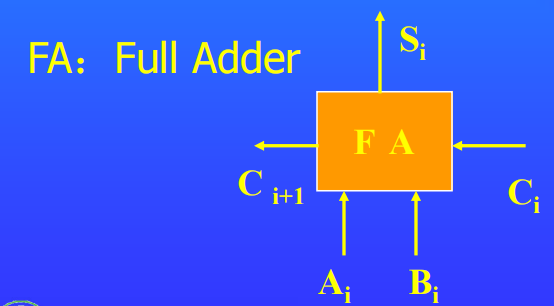
根据真值表，三个输入端和两个输出端可按如下逻辑方程进行联系：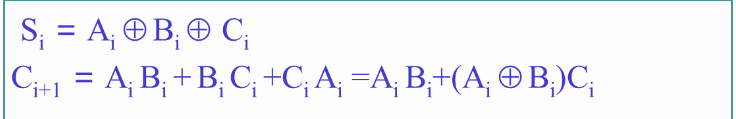

门电路的延迟时间：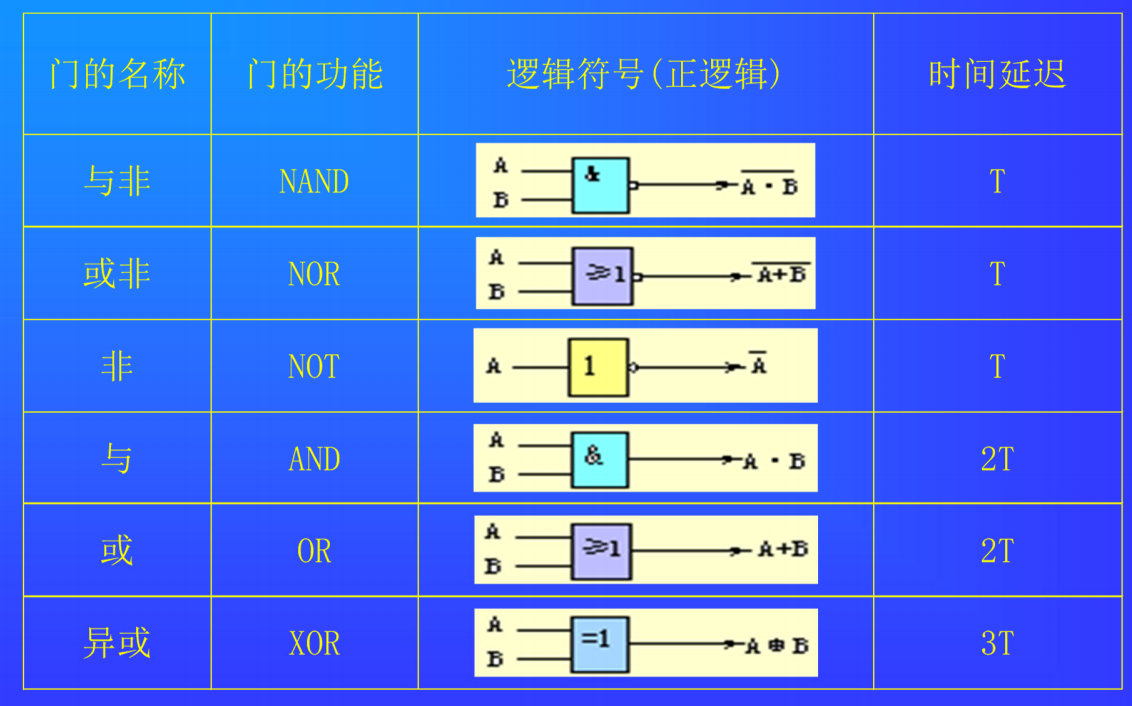

串行加法器

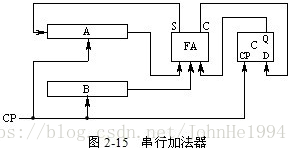
在串行加法器中，只有一个全加器，数据逐位串行送入加法器进行运算，如图所示：图中FA是全加器，A、B是两个具有右移功能的寄存器，C为进位触发器。
由移位寄存器从低位到高位逐位串行提供操作数相加。如果操作数长n位，加法就要分n次进行，每次产生一位和，并串行地送回A寄存器。进位触发器用来寄存进位信号，以便参与下一次的运算。

串行进位加法器

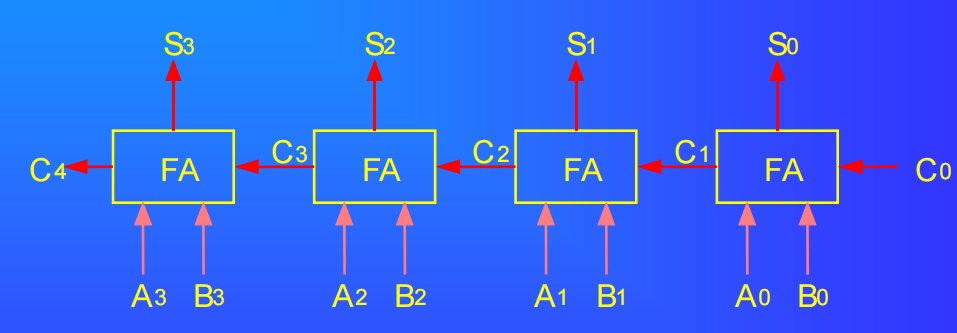
并行加法器中的每一个全加器都有一个从低位送来的进位输入和一个传送给高位的进位输出。通常将传递进位信号的逻辑线路连接起来构成的进位网络称为进位链。每一位的进位表达式为：
$C_i=A_iB_i+(A_i⊕B_i)C_{i-1}$

串行进位并行补码加减法器

n个1位的全加器(FA)可级联成一个n位的行波进位加减法器
M为方式控制输入线：
当M=0时，作加法(A+B)运算；
当M=1时，作减法(A-B)运算，相当于在加法器的最低位上加1。转化成[A]_补 + [-B]_补运算，求补过程由¬[B]_补+1来实现，起始进位连接到M上。
单符号位法的溢出检测逻辑；当C_n\=C_n-1时，运算无溢出
而当C_n≠C_n-1时，运算有溢出，经异或门产生溢出信号。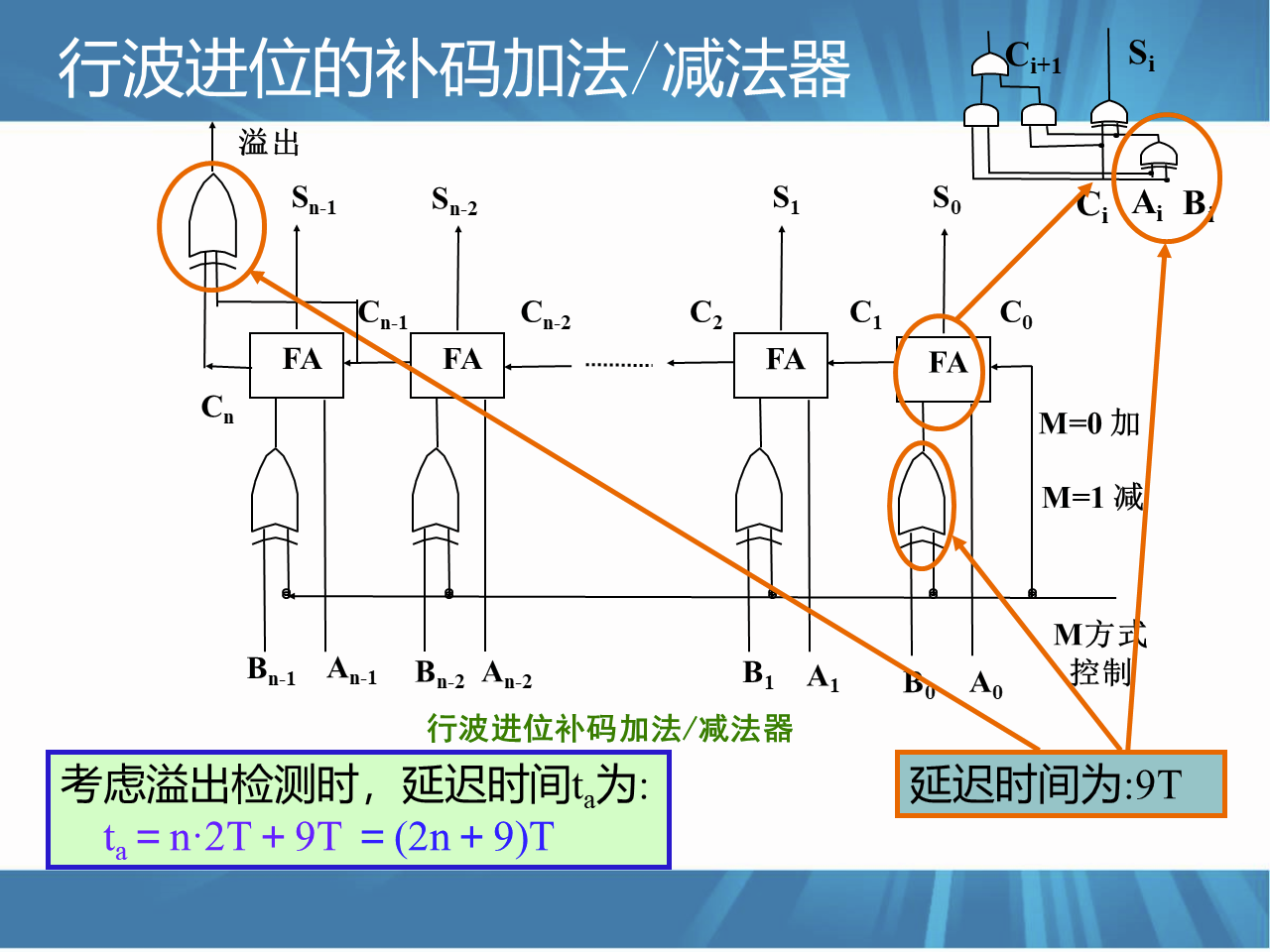

延迟时间计算：

$t=0: A_0\thicksim A_{n-1}, b_0\thicksim B_{n-1}, C_0=M$ 有效
$t=3T: B_i’ = (B_i\enspace xor\enspace M)$ 有效
$t=6T: B_i’\enspace xor\enspace A_i$ 有效
$t=6T + 2T: C1$ 有效
$t=6T + 4T: C2$ 有效
$t=6T + 6T: C3$ 有效
……
$t=6T + 2(n-1)t: Cn-1$ 有效
$t=6T + 2nT: Cn$ 有效
$t=6T + 2(n-1)t + 3T=7T + 2nT: S_{n-1}$ 有效（还需要使用一个异或门）
$t=9T + 2nT:$ 溢出有效

考虑溢出检测的延迟: $t_a=(2n + 9)T$
不考虑溢出检测的延迟: $t_a=(2n + 7)T$

进位产生和传递函数

并行加法器进位链的基本逻辑关系：

$$C_{i+1}=A_iB_i+(A_i⊕B_i)C_i$$

令$G_i=A_iB_i$为进位产生函数（本地进位）
令$P_i=A_i⊕B_i$为进位传递函数（进位条件）
$P_iC_i$为传送进位（条件进位）
于是有：

$$C_{i+1}=G_i+P_iC_i$$

4位先行进位部件(CLA)

16位单极分组先行进位并行加法器

若使用16位串行进位加法器，则总延迟时间为
$t=9T+2nT=9T+2×16T=41T$

多级分组先行进位方式

将若干小组编成一大组

• 小组内为先行进位
• 同一大组内的各小组之间也采用并行进位

一个加法器有一个或多个大组

• 如果有多个大组，每个大组可以既可以使用串行进位，也可以使用并行进位、

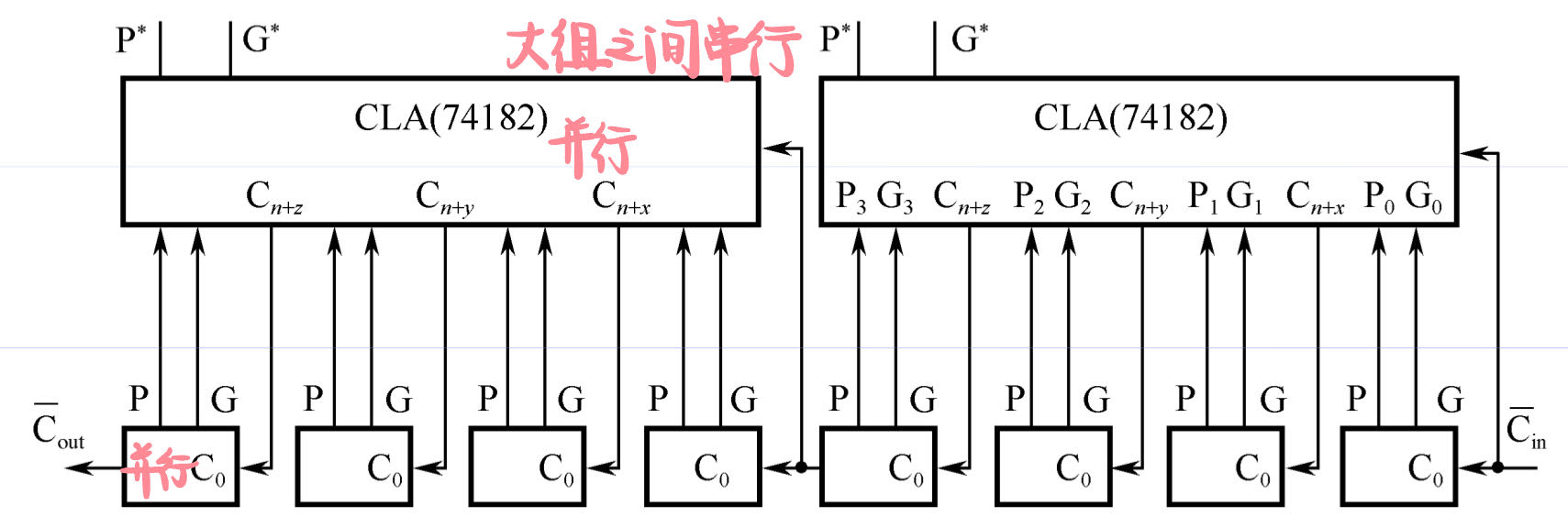
两级分组16位先行进位加法器

先计算 $P^$ 和 $G^$，求出进位，再做加法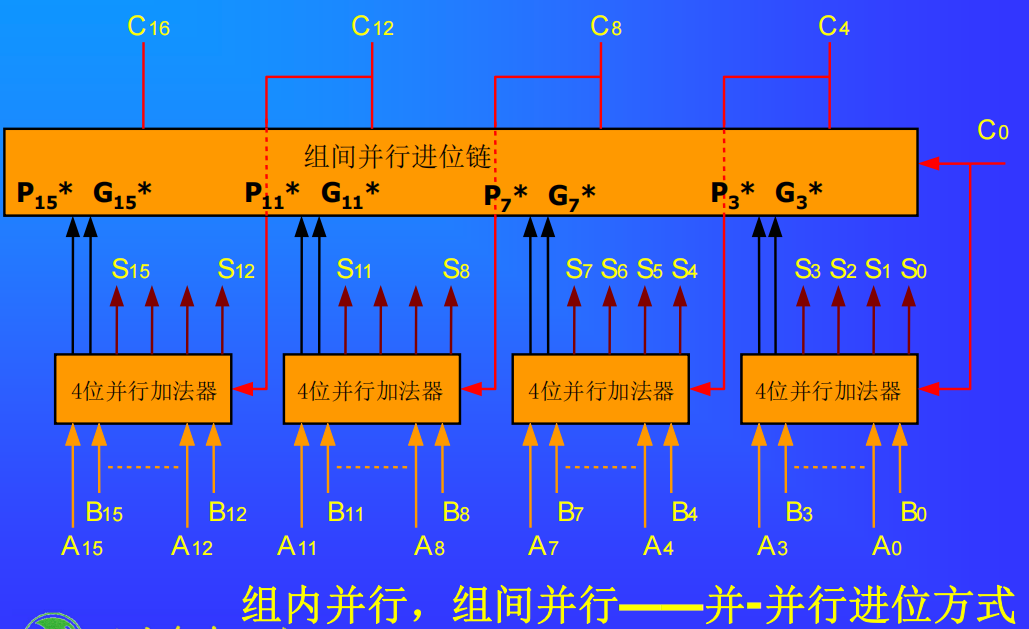

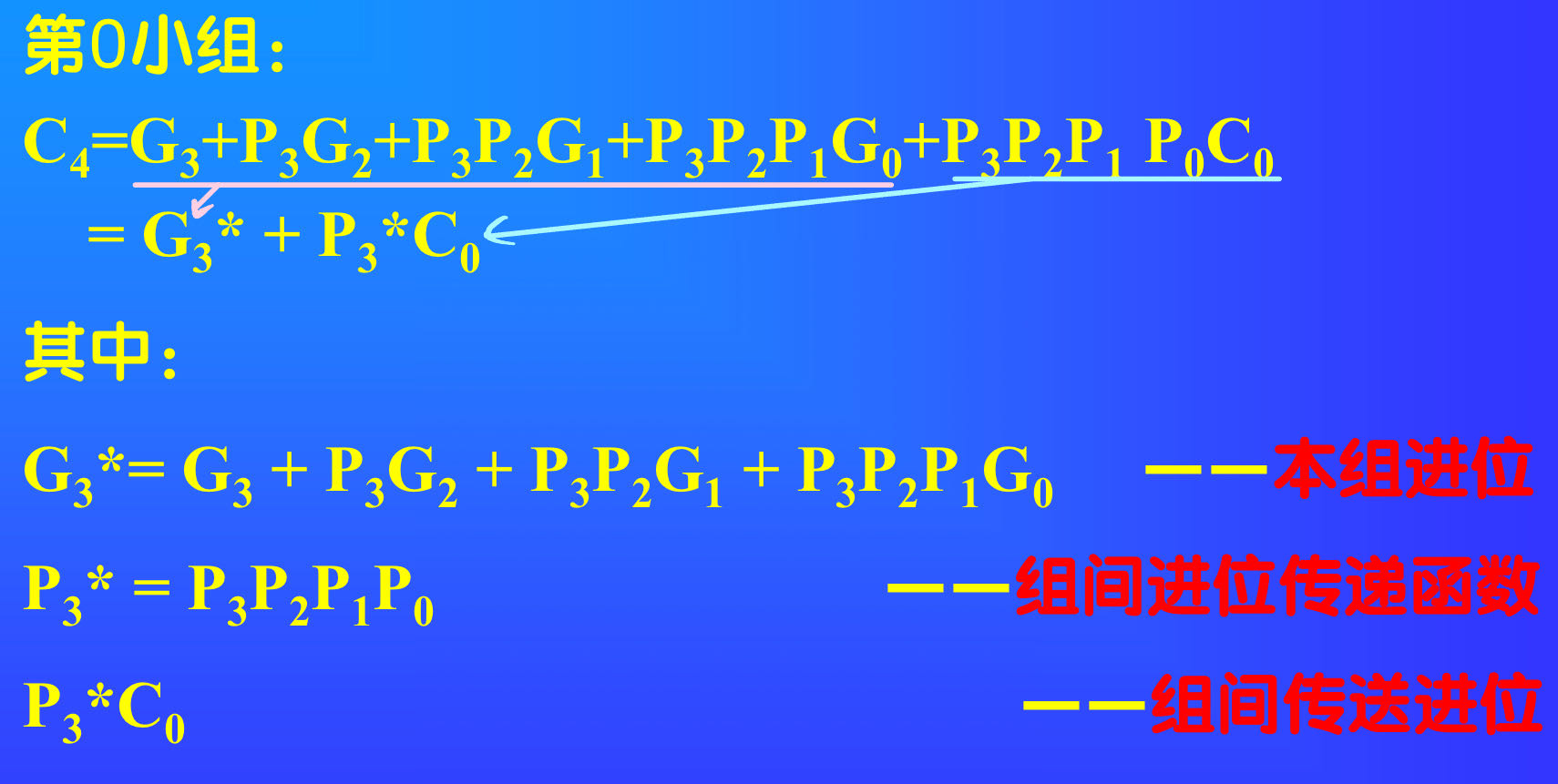
• 组间先行进位逻辑公式
  

  

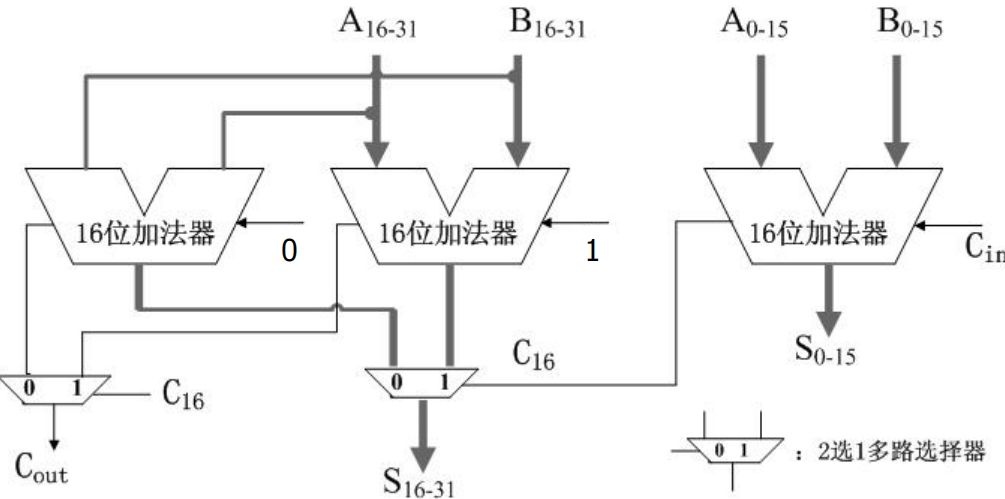
进位选择加法器

定点运算器的组成

• 逻辑运算：
  只在无符号数之间进行逻辑运算
• 逻辑运算和算数运算的区别：
  逻辑运算只在对应的位之间进行
  各位之间没有进位/借位关系
• 计算机中的逻辑运算：逻辑非，逻辑加，逻辑乘，逻辑异

多功能算术/逻辑运算单元(ALU)

四位多功能ALU：74181

引脚介绍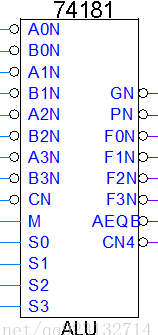

74ls181芯片总共有22个引脚。

• 数据引脚

  • 8个数据输入端，A0m、A1n、A2n、A3n，B0n、B1n、B2n、B3n，（其中A3和B3是高位）。
  • 4个二进制输出端F0、F1、F2、F3，以四位二进制形式输出运算的结果。
  • CN端处理进入芯片前进位值，CN4记录运算后的进位。
  • GN先行进位产生端。PN先行进位传递函数。

• 控制引脚

  • 4个控制端，S0、S1、S2、S3，控制两个四位输入数据的运算，例如加、减、与、或。
  • M控制芯片的运算方式，包括算术运算和逻辑运算。

功能表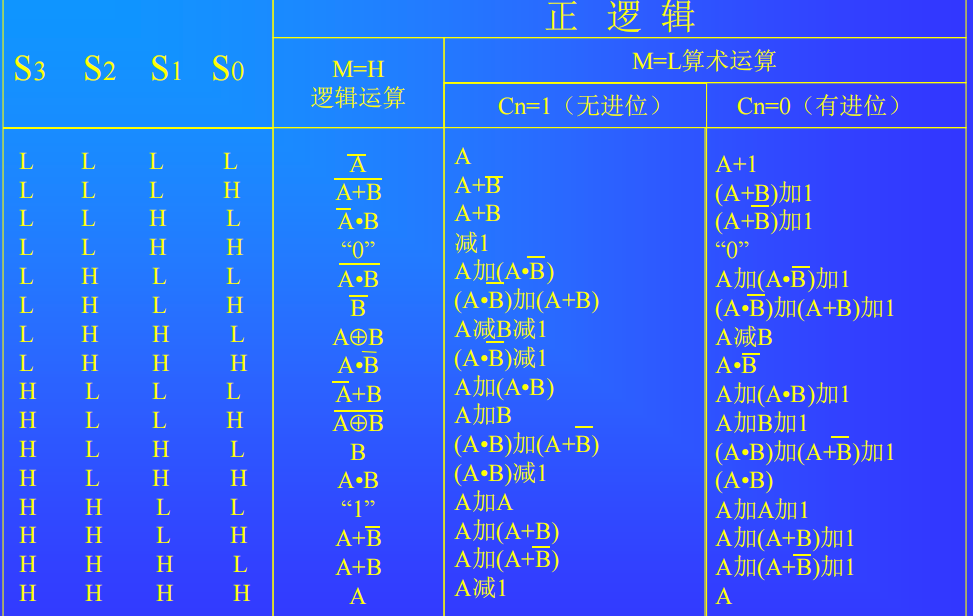

补充：
算术运算操作是用补码表示法来表示的加是指算术加，运算时要考虑进位。
符号“+ ”是指“逻辑加。
减法是用补码方法进行的，其中数的反码是内部产生的，而结果输出“A减B减1”，因此做减法时需在最末位产生一个强迫进位(加1)，以便产生A减B的结果。
A=B输出端可指示两个数相等，因此它与其他ALU的A=B输出端按“与”逻辑连接后，可以检测两个数的相等条件。

超前进位产生器：74182

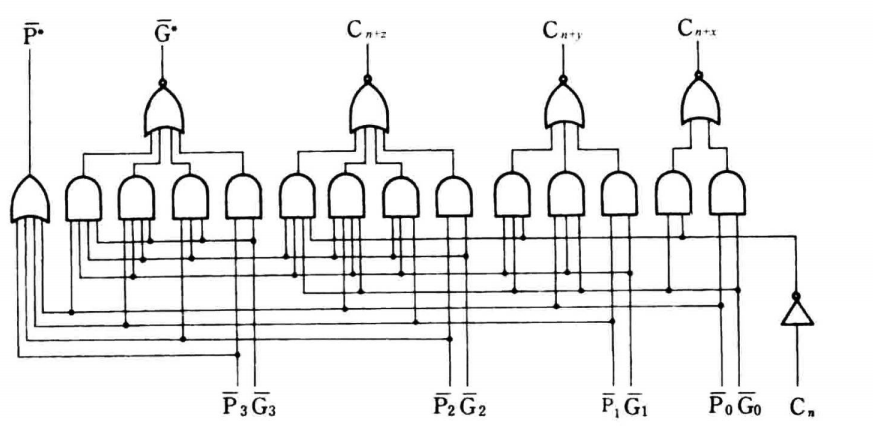
三级分组“并-并-串”先行进位并行ALU